Моделирование монте карло в excel

Надстройка MS Excel «Моделирование Монте-Карло» (Monte-Carlo 6. xla) реализует сбор и обработку информации в книге Excel при статистическом моделировании по методу Монте-Карло.

Результаты представляются в численной и графической форме. Исходные данные для моделирования — любой лист MS Excel, на котором имеются функции, использующие случайные числа.

Отдельный модуль (MCFunctions. xla) содержит набор основных датчиков случайных чисел.

Метод Монте-Карло придуман практически одновременно с компьютерами и с тех пор пользуется популярностью. Не благодаря точности вычислений (которой он не может похвастаться), а благодаря ясности и прозрачности метода получения этих самых результатов. Идейно метод Монте-Карло схож с методом грубой оценки, которым часто пользуются главы компаний и департаментов, чтобы проверить «точные» данные, представленные финансовыми и аналитическими службами. Точности же метода — 1-2%, если обойтись без фанатизма — для практики более чем достаточно.

На странице “Примеры использования. Надстройка «Моделирование Монте-Карло».” вы можете посмотреть несколько иллюстраций применения метода Монте-Карло. Но прежде, чем смотреть примеры, установите саму надстройку и подключите модуль MCFunctions.xla. В противном случае MS Excel не будет знать, откуда взять функции датчиков случайных чисел и запросит обновление связей с другой книгой MS Excel.
Модуль MCFunctions.xla, хоть и устанавливается в составе надстройки «Моделирование Монте-Карло», не имеет ограничений по времени работы и закачать его можно отдельно. Краткое описание модуля читайте на странице “Надстройка-коллекция «Датчики случайных чисел».”.

Вы можете скачать инсталлятор этой надстройки, воспользовавшись ссылкой снизу. Это полнофункциональная версия надстройки, действующая 30 дней после инсталляции. После этого срока надстройка перестанет загружаться, хотя и останется видимой в списке надстроек.

700 KB

Если что-то неясно, можете посмотреть руководство по установке (). Руководство общее для всех надстроек, так как процедуры установки одинаковые.

Купить надстройку можно при посредничестве сайта SoftKey. ru. Стоимость ее невелика, если этот инструмент вам нужен, а точную цену можно узнать кликнув ссылку Купить надстройку.

Изменения в новой версии:

31.10.08 В версии 6.0 изменен интерфейс надстройки. Добавлена возможность отключить вывод гистограмм и кумулят, что полезно при поиске оптимального значения параметра. Для удобства пользователя диапазоны ячеек в полях ввода теперь показываются без названия листа и знаков $.

Имитационное моделирование методом Монте-Карло.

Предлагаю вашему вниманию шаблон для анализа инвестиционного проекта методом Монте-Карло.

Предлагаемый шаблон на основе анализа инвестиционного проекта служит иллюстрацией реализации метода моделирования получившим название «Монте-Карло». Название метода говорит само за себя: в основе моделирования будущих событий лежит использование большого количества случайных величин.

Подобный метод моделирования событий приемлем в тех случаях, когда существует неопределенность относительно значений тех или иных величин.

Считается, что данный метод был использован в работах над атомной бомбой, когда пытались рассчитать количество обогащённого урана необходимое для производства заряда. Слишком маленькое количество могло не дать развиться цепной реакции, а слишком большое было чревато дополнительными месяцами работы над получением необходимого количества урана.

Итак, мы имеем инвестиционный проект, который будет реализован в течение, предположим, 5 лет.

Нам точно не известна цена за которую мы будем реализовывать нашу продукцию, неизвестно точное количество продукции и неизвестно точное значение переменных затрат на ее производство. Это будут случайные величины.

Однако экспертным путем мы определили некий диапазон, в котором будут лежать эти значения.

Например, цена будет не ниже 30 руб. и не выше 40 руб., количество не меньше 150 и не больше 300 единиц, переменные затраты в диапазоне 15 до 20 руб. Цифры могут быть совершенно различными. Важно то, что мы имеем представление о диапазоне их вероятных значений.

Именно значения в этих диапазонах мы и будем моделировать для оценки общей привлекательности проекта.

Для генерации случайных величин мы будем использовать функцию СЛУЧМЕЖДУ, с указанием в качестве аргументов нижней и верхней границы диапазона.

Полученные величины будут использоваться для расчета денежных потоков и чистой приведенной стоимости проекта (NPV).

Генерируется достаточно большое количество вариантов (опытов) и все они обрабатываются методами статистического анализа. В нашем шаблоне мы используем 5 000 опытов, но их может быть и 1 000 000, правда кардинально на результаты это не повлияет.

Это основная философия данного метода. Далее лишь техника реализации.

На листе «Имитация» указываем диапазоны изменения величин, указываем постоянные параметры проекта, а также формируем таблицу в 5 000 строк.

В каждой строке у нас есть случайное значение объема производства, переменных затрат и цены реализации. Также по каждой строке на основе этих данных рассчитываются такие показатели как выручка, прибыль (за минусом постоянных расходов и налога), денежный поток и чистая приведенная стоимость проекта за 5 лет с учетом заданной ставки дисконтирования.

Далее переходим к анализу полученных результатов.

На листе «Результаты анализа» выводим значение минимума, максимума, среднего значения, стандартного отклонения и коэффициента вариации интересующих нас показателей.

По большому счету, нас интересует показатель NPV.

Для него мы рассчитываем также количество случаев, когда NPV 0 для всей совокупности в 5000 опытов.

Вместе с сумой убытков и суммой доходов, эти значения могут дать представление о мере рискованности проекта и масштабе возможных потерь.

Далее, используя стандартное распределение оцениваем вероятность получения того или иного значения NPV. Например, безубыточный проект имеет NPV > 0.

Установив в качестве значения Х (это наше NPV) ноль, мы получим вероятность получения убытка в 3%.

Для определения вероятности используем функцию НОРМ.СТ.РАСП, имеющую следующий синтаксис:

Z Обязательный. Значение, для которого строится распределение.

Интегральная Обязательный. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМ.СТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.

Для определения значения Z используем функцию НОРМАЛИЗАЦИЯ, имеющую следующий синтаксис:

=НОРМАЛИЗАЦИЯ(x, среднее, стандартное_откл)

x Обязательный. Нормализуемое значение. В нашем случае это NPV.

Среднее Обязательный. Среднее арифметическое распределения.

Стандартное_откл Обязательный. Стандартное отклонение распределения.

Среднее значение и стандартное отклонение для NPV мы рассчитали в таблице «Результаты анализа».

Метод Монте-Карло в Excel

ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ МЕТОДОМ МОНТЕ-КАРЛО
Один из самых прикладных методов статистической оценки риска. К нему нужно отнестись с большим участием. В данной статье будет рассмотрен пример имитационного моделирования с использованием данного подхода.

Метод Монте-Карло получил своё название за то, что предназначен осуществить оценку предельно случайных событий. А что, как ни казино, которых в Монте-Карло много, связано со случайностью больше всего?

В процессе работы нам понадобится «генератор случайных чисел» из MS Excel и функция «Описательная статистика».

Оценка риска инвестиционного проекта

Есть следующие условия задачи:

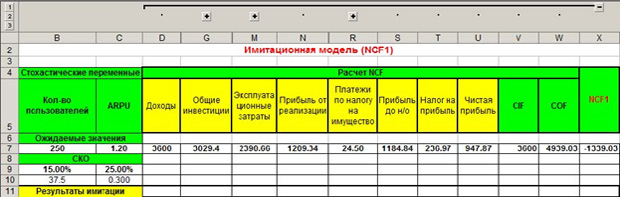
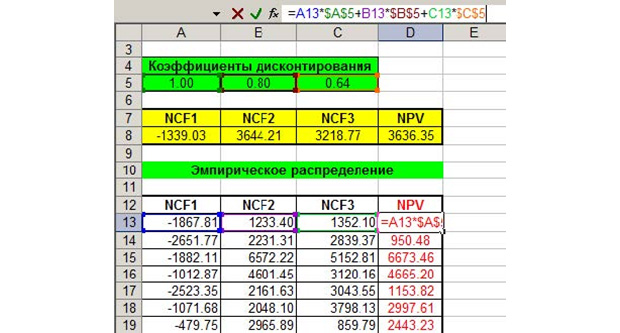
Таким образом, нам нужно оценить три периода – за три года. Запишем все исходные данные в таблицу. Значения, полученные в ячейках D5-X5, имеют формулу для вычисления или есть в условиях задачи. Вы, как экономист, с формулами должны быть знакомы. Обратите внимание на заголовок, выделенный красным цветом на рисунке ниже – «Имитационная модель NCF1». Это говорит о том, что мы имитируем первый год, а всего их будет три на разных листах в MS Excel. На новый лист переключиться внизу окна программы.

Теперь в MS Excel переключаемся на «Данные» и выбираем пункт «Анализ данных».

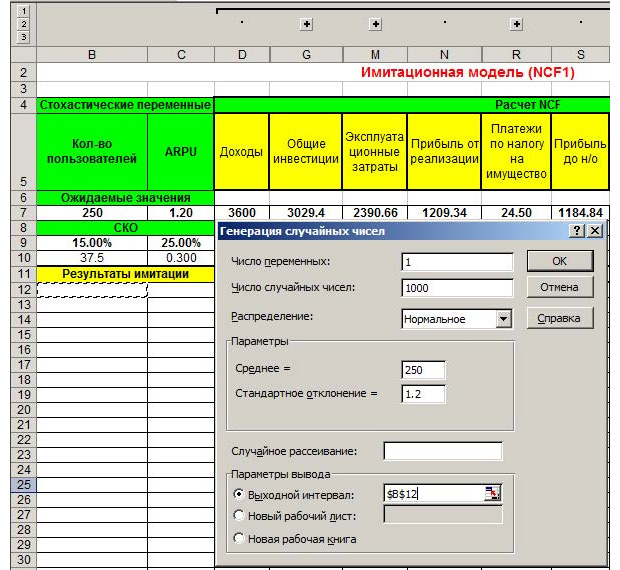
В появившемся окне выбираем «Генерация случайных чисел». Выполняем генерацию с параметрами, продемонстрированными на картинке ниже, для пункта «Кол-во пользователей».

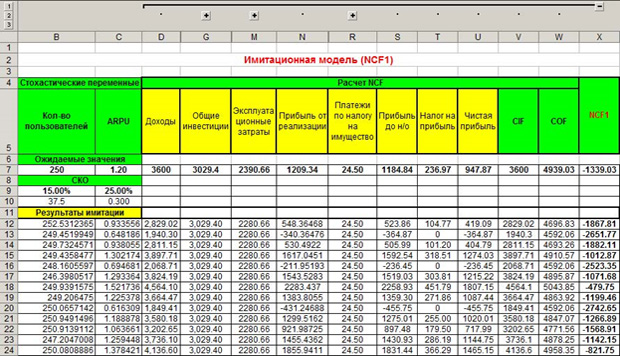
Параметры будут отталкиваться от среднего значения 250, оно есть в ожидаемых значениях в нашей таблице. Нужно выполнить 1000 генераций. Если вы знакомы со статистикой, то понимаете, что большее количество испытаний даёт более точную оценку. Используя метод Монте-Карло, можно имитировать и 10 000 значений для большей точности.

После мы имитируем все стохастические, то есть, меняющиеся значения по аналогии, как показано выше. Копируем формулы переменных или констант из ячеек D7-X7 под «Результаты имитации» с учетом имитированных значений. Получаем следующий результат.

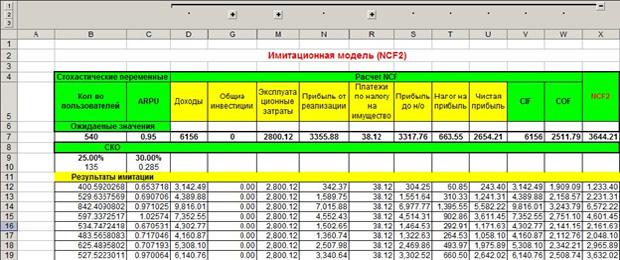
Как видим, платежи по налогам за имущество, например, являются постоянным значением на весь год, поэтому это значение везде одинаковое, а другие меняются, потому что рассчитываются по формулам, и в эти формулы входят меняющиеся значение, имитированные нами. Не забывайте, что значений в каждом столбце должно быть по тысяче.

Теперь делаем то же самое, но для имитационной модели NCF2.

Это второй год работы проекта. Как видим, под «СКО» процентные соотношения увеличились. Об этом говорится в условии задачи, что налоги и зарплата должны расти каждый год.

Повторяем это действие в третий раз, увеличивая налоги и зарплаты, как говорит условие.

Наибольшую важность в оценке инвестиционного проекта имеет параметр NCF – чистый денежный поток. Копируем все значения NCF на четвертый лист с каждой из трёх предыдущих страниц.

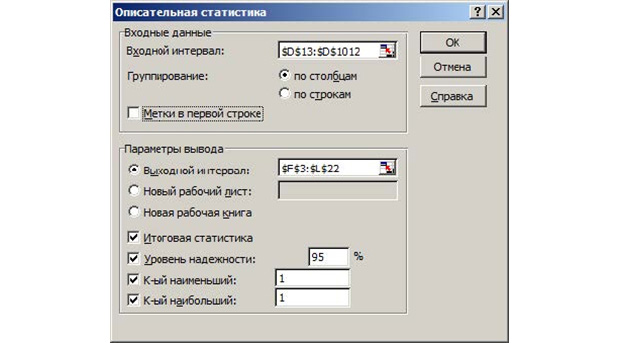
Формула для расчета NPV есть вверху картинки. Используем её. Теперь точно так же заходим в «Данные», жмём на «Анализ данных» и выбираем там «Описательная статистика». Вот, что в появившемся окне вам нужно указать.

Во входном интервале выбирается 1000 полученных значений NPV. Выходной интервал можете выбрать произвольно. На выходе у вас будет таблица со статистическими данными.

Вы, как экономист, должны понимать, о чем говорит каждое значение, если нет, то нужно прочитать отдельную статью или главу учебника. Наша статья о том, метод Монте-Карло применяется с использованием функций MS Excel.

Заключение

Генерация случайных чисел – наше всё. Именно в оценке того, к чему может привести случайность, заключается статистический метод Монте-Карло. Это работает не только в экономике, но и везде, где есть случайность. Можете посмотреть, как это делается, применительно к зоологии в видео ниже.

Talkin go money

RuleOfThumb — Метод Монте-Карло (Апрель 2020).

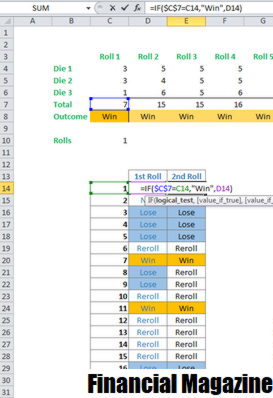
Table of Contents:

Мы разработаем симуляцию Монте-Карло с использованием Microsoft Excel и игра в кости. Моделирование Монте-Карло — математический численный метод, который использует случайные ничьи для выполнения вычислений и сложных проблем. Сегодня он широко используется и играет ключевую роль в различных областях, таких как финансы, физика, химия, экономика и многие другие.

Моделирование Монте-Карло

Метод Монте-Карло был изобретен Николаем Метрополисом в 1947 году и направлен на решение сложных проблем с использованием случайных и вероятностных методов. Термин «Монте-Карло» происходит от административного района Монако, широко известного как место, где европейские элиты играют в азартные игры. Мы используем метод Монте-Карло, когда проблема слишком сложна и сложна при непосредственном вычислении. Большое количество итераций позволяет моделировать нормальное распределение.

Метод моделирования методом Монте-Карло вычисляет вероятности для интегралов и решает уравнения в частных производных, тем самым вводя статистический подход к риску в вероятностном решении. Несмотря на то, что существует множество современных статистических инструментов для создания симуляций Монте-Карло, проще моделировать нормальный закон и единообразный закон с использованием Microsoft Excel и обходить математические основы.

Для моделирования Монте-Карло мы выделяем ряд ключевых переменных, которые контролируют и описывают результат эксперимента и назначают распределение вероятности после выполнения большого количества случайных выборок. Давайте возьмем игру в кости как модель.

Игра в кости

Вот как игра в кости играется:

• Игрок бросает три кости, которые имеют 6 сторон 3 раза.

• Если общее количество 3 бросков составляет 7 или 11, игрок выигрывает.

• Если общее количество 3 бросков: 3, 4, 5, 16, 17 или 18, проигрыватель проигрывает.

• Если общий результат — любой другой результат, игрок снова играет и повторно свертывает штамп.

• Когда игрок снова бросает кубик, игра продолжается таким же образом, за исключением того, что игрок выигрывает, когда сумма равна сумме, определенной в первом раунде.

Рекомендуется также использовать таблицу данных для генерации результатов. Более того, для подготовки моделирования методом Монте-Карло требуется 5 000 результатов.

Шаг 1: События прокатки в кости

Сначала мы разрабатываем ряд данных с результатами каждого из 3 кубиков для 50 рулонов. Для этого предлагается использовать функцию «RANDBETWEEN (1. 6)». Таким образом, каждый раз, когда мы нажимаем F9, мы генерируем новый набор результатов каротажа. Ячейка «Результат» — это сумма итогов трех рулонов.

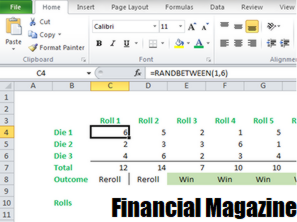
Шаг 2: Диапазон результатов

Затем нам нужно разработать ряд данных для определения возможных результатов для первого раунда и последующих раундов. Ниже приведен диапазон данных с тремя столбцами.В первом столбце у нас есть числа от 1 до 18. Эти цифры представляют собой возможные результаты после того, как катятся кости 3 раза: максимум составляет 3 * 6 = 18. Вы заметите, что для ячеек 1 и 2 результаты N / A, так как невозможно получить 1 или 2, используя 3 кости. Минимальное значение равно 3.

Во втором столбце включены возможные выводы после первого раунда. Как указано в первоначальном заявлении, либо игрок выигрывает (выигрывает), либо проигрывает (проигрывает), либо повторяет его (Re-roll), в зависимости от результата (всего 3 кубика).

В третьей колонке регистрируются возможные выводы для последующих раундов. Мы можем достичь этих результатов, используя функцию «If. «Это гарантирует, что если полученный результат будет эквивалентен результату, полученному в первом раунде, мы выиграем, иначе мы будем следовать первоначальным правилам первоначальной игры, чтобы определить, будем ли мы повторно бросать кости.

Шаг 3: Выводы

На этом этапе мы определяем результат 50 кубиков. Первый вывод можно получить с помощью индексной функции. Эта функция выполняет поиск возможных результатов первого раунда, вывод, соответствующий полученному результату. Например, при получении 6, как это имеет место на рисунке ниже, мы снова играем.

Можно получить результаты других рулонов кости, используя функцию «Or» и функцию индекса, вложенную в функцию «If». Эта функция сообщает Excel: «Если предыдущий результат -« Выиграть или проиграть », перестаньте бросать кости, потому что как только мы выиграли или проиграли, мы закончили. В противном случае мы переходим к столбцу следующих возможных выводов, и мы определяем вывод результата.

Шаг 4: Количество рулонов кости

Теперь мы определяем количество бросков кубиков, необходимых до проигрыша или выигрыша. Для этого мы можем использовать функцию «Countif», которая требует, чтобы Excel подсчитывал результаты «Re-Roll» и добавлял номер 1 к ней. Он добавляет один, потому что у нас есть один дополнительный раунд, и мы получаем окончательный результат (выигрываем или проигрываем).

Шаг 5: Моделирование

Мы разрабатываем диапазон для отслеживания результатов различных симуляций. Для этого мы создадим три столбца. В первом столбце одна из приведенных цифр — 5 000. Во второй колонке мы будем искать результат после 50 кубиков. В третьем столбце, в заголовке столбца, мы будем искать количество бросков кубиков, прежде чем получить окончательный статус (выиграть или проиграть).

Затем мы создадим таблицу анализа чувствительности с использованием данных характеристик или таблицы данных таблицы (эта чувствительность будет вставлена ​​во вторую таблицу и в третьи столбцы). В этом анализе чувствительности номера событий 1 — 5, 000 должны быть вставлены в ячейку A1 файла. Фактически, можно было выбрать любую пустую ячейку. Идея состоит в том, чтобы просто произвести перерасчет каждый раз и таким образом получить новые броски кубиков (результаты новых симуляций), не повредив формулы на месте.

Шаг 6: Вероятность

Мы можем, наконец, вычислить вероятности выигрыша и проигрыша. Мы делаем это с помощью функции «Countif».Формула подсчитывает количество «выигрышей» и «проиграет», а затем делит на общее количество событий, 5, 000, чтобы получить соответствующую долю одного и другого. Наконец, мы видим, что вероятность получить выигрыш составляет 73. 2%, а результат Lose — 26,8%.

Оценка статьи:

Загрузка...